- Research
- Open access
- Published:
Efficient algorithms for the discovery of gapped factors
Algorithms for Molecular Biology volume 6, Article number: 5 (2011)
Abstract
Background
The discovery of surprisingly frequent patterns is of paramount interest in bioinformatics and computational biology. Among the patterns considered, those consisting of pairs of solid words that co-occur within a prescribed maximum distance -or gapped factors- emerge in a variety of contexts of DNA and protein sequence analysis. A few algorithms and tools have been developed in connection with specific formulations of the problem, however, none can handle comprehensively each of the multiple ways in which the distance between the two terms in a pair may be defined.
Results
This paper presents efficient algorithms and tools for the extraction of all pairs of words up to an arbitrarily large length that co-occur surprisingly often in close proximity within a sequence. Whereas the number of such pairs in a sequence of n characters can be Θ(n4), it is shown that an exhaustive discovery process can be carried out in O(n2) or O(n3), depending on the way distance is measured. This is made possible by a prudent combination of properties of pattern maximality and monotonicity of scores, which lead to reduce the number of word pairs to be weighed explicitly, while still producing also the scores attained by any of the pairs not explicitly considered. We applied our approach to the discovery of spaced dyads in DNA sequences.
Conclusions
Experiments on biological datasets prove that the method is effective and much faster than exhaustive enumeration of candidate patterns. Software is available freely by academic users via the web interface at http://bcb.dei.unipd.it:8080/dyweb.
Background
The computation of statistical indexes containing subword frequency counts, expectations, and scores thereof, arises routinely in the analysis of biological sequences. This problem is usually manageable when the word length is limited to some fixed, small value but rapidly escalates in complexity when applied on a genomic scale, perhaps without any length bound. In principle, a sequence of n characters may contain Θ(n2) distinct substrings, whence an exhaustive statistical index would be by one order larger than its subject. In previous work by [1], the size of such exhaustive tables has been shown to reduce to O(n) by a prudent combination of properties related to pattern maximality and monotonicity of scores. In informal terms, maximal substrings in a sequence may be obtained by partitioning all sub-strings into equivalence classes, in such a way that the strings in each class share precisely the same set of starting positions in that sequence. Thus, every word in a class must be a prefix of some maximal word w, that together with the list of occurrences represents the entire class. A classical result bounds the number of such representatives by O(n). In addition, it has been shown that the z-scores or departure from expected occurrence count of the elements in each class are monotonically increasing. This allows one to score only the representative in each class, since any other word in that class is a prefix of, and not more surprising than, the representative. Similar conservative approaches have been already applied successfully to patterns affected by indeterminacies of various kinds [2, 3].
In this paper, we consider the problem of exhaustive counting and discovery of pairs of subwords that co-occur more frequently than expected within a specified distance in a sequence. In the literature, these patterns are also refered to as gapped factors.
In [4], and [5], indexes are proposed to solve the problem of searching a text for an assigned gapped-factors query. The problem of discovering such signals is intrinsically more difficult than searching, since no specific query is provided as input, and all candidate patterns must be weighed by some score of statistical significance.
Within the bioinformatics literature, algorithms from [6–9], have been proposed for the closely related problem of discovering composite motifs. These are indeed combinations of two or more approximate signals that may not have an exact occurrence in the input sequences. Hence those algorithms have been designed to compute a slightly different statistic than ours. In [10] the exhaustive enumeration of gapped factors has been proposed for the detection of dyadic transcription factors.
In contexts other than bioinformatics, a generalization of gapped factors was addressed in [11] under the name of word association pattern, which refers to a tuple of k components matching the input string within distance d. The algorithm takes time O(dknk+1log n), which reduces to our problem by setting k = 2, yielding time O(d2n3 log n), or O(n3 log n) when d is a constant. A related algorithm was also proposed in [12], running in time O(n3) but requiring O(n2) scans of the input string, for the case of gapped factors.
We show that O(n2) time and space suffices to build and represent this kind of statistical index using a compact approach for both head-to-head and up to d head-to-tail distances. An additional linear factor is to be charged when dealing with up to d tail-to-head distance or if d is a parameter. Furthermore, the computation of z-scores can be included in our constructions within the same complexity bounds.
Our presentation is organized as follows. We first recapture previous results on optimal count for gapped factors within head-to-head distance, and then present algorithms dealing with other distance measures between factors. We also show how to incorporate in the computation z-scores, extending the framework to a discovery process based on over-representation, and the space savings induced by their monotonicity within gapped factors equivalence classes.
Finally, we test our approach on the problem of discovering spaced-dyads and compare the efficiency and efficacy of our compact approach with respect to the exhaustive enumeration of [10].
Methods
Problem statement
Let x be a string over some alphabet Σ, where |x| = n, and let d be some fixed non-negative integer. Given two strings y and z that occur in x, the triplet (y, z, d) defines a gapped factor where y is the first component, z is the second component, and it is asked that they co-occur at a distance less than or equal to d. When d is fixed we just refer to the pair of factors (y, z). For any pair (y, z) of strings in x, the co-occurrence count is the number of times an occurrence of z follows an occurrence of y within a distance d. The variety of ways in which the distance between components may be measured leads to several variants for the problem, as exemplified in Figure 1, 2, and 3.
Definition 1. The basic head-to-head index I HH (y, z) relative to x is the number of times that z has an occurrence in x within a distance d from an occurrence of y to its left.
Definition 2. The basic tail-to-head index I TH (y, z) relative to x is the number of times that z has an occurrence in x within a distance d ≥ 0 from the last symbol of an occurrence of y to its left.
Definition 3. The basic head-to-tail index I HT (y, z) relative to x is the number of times that z has an occurrence in x which ends within a distance d from a corresponding occurrence of y to its left.
We can also require that no interleaving occurrence of one or the other factor occurs between the considered occurrences of y and z. We then talk about the relaxed tandem index Î(y, z), and the tandem index I(y, z), for which the head-to-head distance are defined as follows.
Definition 4. The relaxed tandem index Î(y, z) relative to x is the number of times that z has an occurrence in x within head-to-head distance d from a corresponding, closest occurrence of y to its left.
Definition 5. The tandem index I(y, z) relative to x is the number of times that z has a closest occurrence in x within head-to-head distance d from a corresponding, closest occurrence of y to its left.
We illustrate the definitions of tandems for head-to-head distance in Figure 4.
Let p i and pi+1be the starting positions of the only two occurrences of y in an input sequence, and let q k , qk+1and qk+2be the starting positions of the only three occurrences of z. Let d be the maximum distance allowed for co-occurrences, as sketched in Figure 4. The basic head-to-head index for (y, z) is I HH (y, z) = 4: three co-occurrences corresponding to the occurrence of y at p i and one corresponding to the occurrence of y at pi+1. Hence, the set of co-occurrences is {(p i , q k ), (p i , qk+1), (p i , qk+2), (pi+1, qk+2)}.
To obtain the relaxed tandem index Î(y, z) only the occurrences of z that fall within distance d from an occurrence of y, but before the next occurrence of y, are counted. In the case of Figure 4 this produces a contribution of two pairs for the first occurrence of y, and one for the second. In fact, the last occurrence of z is now counted only once, in association with its closest occurrence of y at pi+1.
Finally, to obtain the tandem index I(y, z), one more adjustment is needed, since now only one of the two occurrences of z that pair up with p i is to be counted, namely, the closest one. This yields the final value of I(y, z) = 2, from the two co-occurrences {(p i , q k ) and (pi+1, qk +2)}.
Algorithms
Here we present algorithms to count and discover the various kinds of gapped factors defined in the previous section. The index for computing I HH with and without interleaving occurrences was first introduced in [3]. We add to this the description of notable variants and the discovery frameworks.
As it was mentioned earlier, since there may be Θ(n2) distinct substrings in x, then the number of possible gapped factors, either interleaving or not is Θ(n4), and such is the time necessary for their exhaustive enumeration. Our algorithms exploit some properties of the suffix tree data structure to reduce this complexity. A suffix tree T x of an input string x defined over an alphabet Σ is a compact trie of all the suffixes of x$, where $ is a special symbol that does not belong to Σ. Suffix trees can be constructed in time linear in the length of the input string. We refer to [13–15] for detailed constructions. In our discussion, we use the letters v, x, y, and z to denote strings, and the letters α and β for nodes of the tree. The word ending precisely at vertex α of T x is denoted by w(α), and α is called the proper locus of w(α). The locus of a substring v of x is the unique vertex α of T x such that v is a prefix of w(α) and w(Father(α)) is a proper prefix of v.
Suffix trees enjoy several interesting properties [16, 17]. In particular, since in any such tree there are exactly n leaves (one for each suffix) and each internal node is a branching node, then the total number of nodes is linear. By the structure of the tree, the occurrences of a word v start precisely at the suffixes that are found in the subtree rooted at the locus of v. Thus, any word v ending in the middle of an arc will have the same starting positions, and consequently the same number of occurrences, as the word w(α) with α the locus of v (see Figure 5).
Counting Gapped Factors: Head-to-Head distance
The O(n) words ending at the branching nodes and leaves of the suffix tree represent a compendium of all the substrings of the input string x, and each node or leaf represents an equivalence class, in the sense that strings with the same locus share the same set of starting positions. Clearly, it is enough to consider as factors only pairs of class representatives, where the representative of a class is the longest string in that class. For any pair of words (y', z') not explicitly considered, there exists another pair (y, z), formed by representatives, hence such that y' is a prefix of y, and z' is a prefix of z, and the two pairs have the same number of co-occurrences as shown in Figure 6. Hence, for a given query (y', z') we can report as result the value of I HH (y, z).
The occurrences for gapped factors that, within a given distance d, have a fixed string y as their first component are computed in three steps as follows:
-
a)
Consider the starting positions p 1, p 2,..., p k of all occurrences of y in x, where y = w(α) and α is a node in T x ,
-
b)
Let L be the mapping leading from each sequence position to the corresponding leaf node, and give a weight to each leaf, initially set to zero. For each p i mark the positions p i + 1, p i +2,... p i +d, and add one to the weight of the corresponding leaf nodes {L(p i +1), L(p i + 2),..., L(p i + d)};
-
c)
Traversing the tree bottom-up, annotate each internal node β with the sum of the weights of the children nodes.
Upon completion, the generic node β of the tree holds the value of I HH (y, z), where z = w(β). The annotation of the tree for a fixed y takes O(n) time if d is fixed. Since this has to be repeated for each one of the O(n) choices of the first component y, then the overall execution time is O(n2). Indeed, with a properly tuned construction of the index, the time can be linear in the output size [18].
Counting Gapped Factors: Tail-to-Head distance
When we consider tail-to-head distance, we cannot directly apply the previous method and just add a shift of length |y| to the marking phase. In fact, the prefix y' of y, that has the same locus α in the tree as y will be at a tail-to head distance from a certain z larger than the distance between y and z. Thus, when we mark the positions p i + |y| + j - 1, 1 ≤ j ≤ d, as in Figure 7 some positions (those falling in segment A) that should be marked for y' will not be marked, and some other (those falling in segment B) that should not be marked for y' will be actually marked. Note that even though A and B have clearly the same length the strings that they intercept are generally different.
This problem is overcome by building, in time and space O(n3), the index  between maximal strings for all possible non negative exact distances h. The index is built as follows:
between maximal strings for all possible non negative exact distances h. The index is built as follows:
-
a)
Consider the starting positions p 1, p 2,..., p k of all occurrences of y in x, where y = w(α) and α is a node in T x ;
-
b)
Let L be the mapping leading from each sequence position to the corresponding leaf node, and give a weight to each leaf, initially set to zero. For each p i add one to the weight of the leaf node L(p i + |y| + h);
-
c)
Traversing the tree bottom-up, annotate each internal node β with the sum of the values of the children.
At the end of this computation the generic node β of the tree holds the value of  where z = w(β). The annotation of the tree for a fixed y and h takes O(n) time. This process needs to be repeated for every distance 0 ≤ h < n and for every choice of the first component y, taking overall O(n3) time and space.
where z = w(β). The annotation of the tree for a fixed y and h takes O(n) time. This process needs to be repeated for every distance 0 ≤ h < n and for every choice of the first component y, taking overall O(n3) time and space.
This set of trees can then be used to compute the tail-to head index between any two strings, not necessarily maximal, occurring in the sequence. Let y' and z' be two strings that have respectively y and z as the strings corresponding to their loci. For a query I
TH
(y', z') within distance d one needs to compute  , 0 ≤ h ≤ d. For each h we need to distinguish two cases:
, 0 ≤ h ≤ d. For each h we need to distinguish two cases:
-
1.
|y'| + h > |y|: the occurrences of the corresponding maximal strings y and z do not overlap, hence
 (see Figure 8).
(see Figure 8).
-
2.
|y'| + h ≤ |y|: the occurrences of the corresponding maximal strings y and z overlap. Let w be the string given by the concatenation with overlap of y and z' (see Figure 9): y 1 ... y |y'|+h· z'. We can get the number of co-occurrences directly by searching the occurrences of w in the suffix tree.
The time required by these two operation is O(|y| + |z'|). The tail-to-head index is finally given by  .
.
Counting Gapped Factors: Head-to-Tail distance
This case consists of gapped factors in which the distance is measured from the beginning of the first component to the end of the second.
The case of head-to-tail distance is a very special case. In fact here we are interested in counting the number of strings that fall completely within a bounded distance d from the beginning of the first component.
Let us build the suffix tree for the input sequence. For a first component y = w(α), occurring at n
y
positions  in x we consider the set of substrings {x[p
i
+ 1, p
i
+ d - 1], i = 1.. n
y
}. We then build a generalized suffix tree for
in x we consider the set of substrings {x[p
i
+ 1, p
i
+ d - 1], i = 1.. n
y
}. We then build a generalized suffix tree for  , where each $
i
is an end-marker ($
i
≠ $
j
if i ≠ j) needed to correctly compute the index. The total length of these strings, and so the order of the number of nodes in the tree, is (d + 1) × n
y
.
, where each $
i
is an end-marker ($
i
≠ $
j
if i ≠ j) needed to correctly compute the index. The total length of these strings, and so the order of the number of nodes in the tree, is (d + 1) × n
y
.
For each string z = w(β), where β is a node of this tree, the count of the number of leaves of the subtree rooted at β will give the number of co-occurrences between y and z at head-to-tail distance d. In this count all the substrings of y are also counted. If we want to avoid to include this obvious type of co-occurrence, we can mark the leaves coming from the positions within the occurrence of y while building the tree, and avoid counting them.
Obviously, if a string z = w(β) is totally contained within distance d from an occurrence of y, so will be any of its prefixes z' with locus β. On the other hand, every prefix y' of y with locus β such that y = w(α) will share with y the same set of starting positions. In the light of these considerations, a general query I HT (y', z') will be answered with the indexed value I HT (y, z).
In terms of time complexity, we have that for each string of the type y = w(α),α ∈ T x with n y occurrences we perform O(d × n y ) operations. This must be repeated for every node α ∈ T x . The number of occurrences of each node are given by the sum of the occurrences of its children. In the worst case (think of the tree for an $) their sum is O(n2). So the total complexity is O(d × n2). Since d is constant, we have O(n2).
Avoiding interleaving occurrences
The computation of the tandem indexes of z and y prescribes that two kinds of intermediate occurrences be avoided, as described next.
Computing the Relaxed Tandem Index
To compute the relaxed tandem index, each oc-currence of z must be referred to its closest occurrence of y to the left. The algorithm to compute the relaxed tandem index is similar to the basic algorithm, where steps (a) and (c) are unchanged, while in step (b) only the positions p i +1, p i +2,... p i + d', where d' = min{d, pi+1- p i - 1} are marked. Time and space complexities of the basic algorithm stay unchanged.
Computing the Tandem Index
To compute the tandem index we first apply steps (a) and (b) for the construction of the relaxed tandem index. Furthermore, for each occurrence p
i
of y we create the list of nodes  . For every pair of consecutive nodes (β
i
, βi+1) in the list, we invoke the LCA algorithm of [19] in order to identify their least common ancestor node β, and we subtract 1 to its weight. This adjustment is needed because in the computation of the relaxed index the longest common prefix z between nodes β
i
and βi+1, rep-resented by node β, has been weighed twice, once from the path that leads to the leaf β
i
, the other from the path that leads to βi+1. This is true also for any node in the path from the root to β. So step (c) is needed to propagate both the weights and the adjustments. The weight of an internal node is then given by the sum of the weights of its children with the possible subtraction of the value weighted during the LCA calls. An example is shown in Figure 10 where the suffixes starting at q
k
and qk+1share the common prefix z = w(β).
. For every pair of consecutive nodes (β
i
, βi+1) in the list, we invoke the LCA algorithm of [19] in order to identify their least common ancestor node β, and we subtract 1 to its weight. This adjustment is needed because in the computation of the relaxed index the longest common prefix z between nodes β
i
and βi+1, rep-resented by node β, has been weighed twice, once from the path that leads to the leaf β
i
, the other from the path that leads to βi+1. This is true also for any node in the path from the root to β. So step (c) is needed to propagate both the weights and the adjustments. The weight of an internal node is then given by the sum of the weights of its children with the possible subtraction of the value weighted during the LCA calls. An example is shown in Figure 10 where the suffixes starting at q
k
and qk+1share the common prefix z = w(β).
The strategy to avoid interleaving occurrences was first presented in [3]. Independently, [20] presented a similar approach to count gapped factors in a set of sequences. In their work the LCA algorithm is used to take into account just one instance per sequence.
Discovering Over-represented Gapped Factors
Let y and z be the first and second factors in a pair, respectively, d the distance between them, and assume that y and z do not overlap. We take the expected frequency of D = (y, z) to be the product of the expected frequencies of the individual terms y and z, formally: F e (D) = f(y)f(z), and consider two possible settings, depending on whether f(y) and f(z) are computed on the input sequence x or on a given external (super)sequence. In both cases it may be argued along the lines of [1] that it suffices to weigh the pairs corresponding to the nearest branching nodes, that correspond to the representatives of equivalence classes the score of which cannot be smaller than that of any other pair from the same classes.
Consider two substrings y' and z' of x with no proper locus in T x . Let α and β be their respective loci, and let y = w(α) and z = w(β) be the corresponding strings (cf. Figure 6).
Clearly, y' and y share the same set of starting positions, and the same holds for z' and z. In fact, this property holds for all pairs of strings having respectively α and β as proper locus. Hence these strings can be said to belong to an equivalence class, let it be denoted by C yz , in the sense that the number of times that they co-occur coincides with the number of times that y and z co-occur. I.e., F c (D') = F c (D), where D' = (y', z') and F c (·) is the frequency count.
Moreover, under i.i.d. hypothesis we have for the expected frequency F e :

In other words, for all gapped factors D' = (y', z') in C yz , the probability of D' = (y', z') is not smaller than that of D = (y, z).
Consider now the following scores comparing expected and counted number of co-occurrences:
-
1.
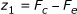
-
2.

-
3.

-
4.

It follows from our discussion that since, moving downward along an arc, F c remains constant while F e is non-increasing, then the value of any such score is non-increasing, whence it is enough to compute it only for pairs of strings having a proper locus.
We conclude that it suffices to score only the representative for each class, since the pair D(y, z) of strings with a proper locus will attain the highest score among members of C yz .
Results and Discussion
As an example application we demonstrate the performance of our method in connection with the discovery of co-occurrences representing transcription factor binding sites. It is known that these sites have a variable structure, although they are all characterized by a high degree of similarity among their oc-currences. Many pattern discovery algorithms (see, e.g., [21] and references therein) assume that the errors are randomly distributed in the pattern. However, this is not necessarily the case. The variability among binding sites might be concentrated at their centers or on their sides. For example, the factor Gal4p, that belongs to the zinc finger class, binds to a pair of conserved regions, separated by a fixed length segment of DNA of variable content. This kind of binding sites are also called a spaced dyad.
In [10], the problem of dyad discovery is solved through an algorithm based on exhaustive enumeration of pairs of components. A significance score is computed with respect to a given background model, and used to rate the dyads. The output is given by the pairs with the highest scores. This approach was proved to be effective in the prediction of such spaced dyads, however, the exhaustive enumeration of dyads, the computation of the background and the scanning of the sequence for each candidate makes the computation imposing and not scalable with the size of the components.
To test our approach on the dyad discovery problem we implemented a simplified version of the head-to-head and tail-to-head algorithms. The software, called DyVerb was developed in Java and it is available via a web interface at http://bcb.dei.unipd.it:8080/dyweb/.
In a direct emulation of the RSAT dyad-analysis tool by [10], we applied DyVerb to the computation of the co-occurrences between all the TST leaves at tail-to-head distance varying from 0 to 16, and the expected frequency of the dyad is given by the product of the counted frequencies of the components. The length of the components was set to 3, and we searched both strands. We then performed two runs of experiments to verify both the efficacy in the discovery of the dyad signals using several scores, and the execution time performance. These experiments are described in the following subsections.
Efficacy of discovery on real datasets
We considered as benchmark the dataset from [10], which consists in 8 gene families that are regulated by zinc-bicluster transcription factors. In Table 1 we report the results in the extraction of spaced dyads based on the scores z2 and z3 and also the significance score defined in [10], with monadic back-ground frequencies taken from the input sequences. For completeness, we report here the definition of the significance score:

where P (D, ≥ n) is the probability of observing at least n occurrences of the dyad D in the input set, and N p is the number of unique spaced dyads in which the components have length 3 and distance varying from 0 to 16.
The table reports, for each set of sequences, the rank of the discovered motif which is closest to the real one, which is represented on the right with the gapped factor discovered by DyVerb highlighted in bold. In most of these tests, DyVerb ranked the gapped factors corresponding to known motifs at the top.
Note that several motifs can score the same value. The table lists such motifs following no particular order. This is irrelevant for most of the experiments, in which indeed the real motif commands the first position. For more subtle motifs such as CAT8, the score z2 ranks the motif as 15th, although the real position in the table is 24th. The value of z3 for the same motif is the 3rd largest, but it appears at the 6th position in the table. Similarly, for the significance score, the motif is 3rd in rank, but shown at the 5th position. We also found that for this motif all scores we computed resulted in similar values. Another subtle motif is HAP1. The best score here appears to be z3, however, for this score only two values were found, namely, 0.002 and 0.001. Nonetheless, only 18 motifs scored 0.002, and among those the gapped factor GGAnnnnnCGG that can be mapped easily to the real motif.
Efficiency of discovery on real datasets
Additional experiments were performed for the purpose of assessing scalability. For this, we implemented exhaustive enumeration using the same programming language (Java) and the same machine (a Pentium4 running at 2.26 GHz with 1 GB of memory) as used for DyVerb. We noted the times required to compute different scores, specifically z2, z3, and Signif, the significance score. Table 2 shows the results of these experiments. It can be seen that for large datasets, such as UME6, the time required by DyVerb is significantly shorter than that required by the exhaustive approach.
Conclusions
In this paper we presented algorithms based a on a conservative approach to the construction of statistical indexes for the discovery of over-represented co-occurrences. The advantage over exhaustive enumeration is in the substantial reduction of the space of candidates, which unlike heuristic approaches, does not pose the risk of missing the optimal ones. The web tool DyVerb was developed to discover dyadic motifs.
Experiments on real datasets showed that the simple probabilistic model used by DyVerb is capable of discovering known signals, in a simple and fast way. Future developments will address on one hand the optimization of the data structures in use, in order to deal with larger sequences, on the other, the implementation of more advanced probabilistic models such as those previously developed in [1] in connection with single patterns.
References
Apostolico A, Bock ME, Lonardi S: Monotony of surprise and large-scale quest for unusual words. Journal of Computational Biology. 2003, 10 (3-4): 238-311. 10.1089/10665270360688020
Apostolico A, Pizzi C: Motif discovery by monotone scores. Discrete Applied Mathematics, special issue Computational Molecular Biology Series. 2007, 155 (6-7): 695-706.
Apostolico A, Pizzi C, Satta G: Optimal discovery of subword associations in strings (extended abstract). Proceedings of the Seventh International Conference on Discovery Science: 2-5 Oct 2004; Padova, Italy. Edited by: Suzuki. 2004, 270-277. Arikawa, Springer, LNAI 3245,
Peterlongo P, Allali J, Sagot MF: Indexing gapped factors using a tree. International Journal on Fundation of Computer Science. 2008, 19: 71-87. 10.1142/S0129054108005541
Iliopoulos CS, Rahman MS: Indexing factors with gaps. Algorithmica. 2007, 55: 60-70. 10.1007/s00453-007-9141-3
Marsan L, Sagot MF: Extracting Structured Motifs Using a Suffix Tree - Algorithms and Application to Promoter Consensus Identification. Proceedings of the Fourth Annual International Conference on Computational Molecular Biology: 8-11 April 2000; Tokyo. Edited by: Shamir, Miyano, Istrail, Pevzner, Waterman. 2000, 210-219. ACM Press,
Eskin E, Pevzner P: Finding composite regulatory patterns in DNA Sequences. Bioinformatics. 2002, 18: 354-363.
Carvalho A, Freitas A, Oliveira A, Sagot M: Efficient extraction of structured motifs using box-links. Proceedings of the 11th Conference on String Processing and Information Retrieval: 5-8 Oct 2004; Padova, Italy. Edited by: Apostolico, Melucci. 2004, 267-268. Springer LNCS 3246,
Pisanti N, Carvahlo A, Marsan L, Sagot MF: RISOTTO: Fast extraction of motifs with mismatches. Proceedings of the LATIN 2006 - Theoretical Informatics, 7th Latin American Symposium: 20-24 March 2006; Valdivia, Chile. Edited by: Correa, Hevia, Kiwi. 2006, 757-768. Springer LNCS 3887,
van Helden J, Rios A, Collado-Vides J: Discovery regulatory elements in non-coding sequences by analysis of spaced dyads. Nucleic Acid Research. 2000, 28 (8): 1808-1818. 10.1093/nar/28.8.1808
Arimura H, Arikawa S: Efficient discovery of optimal word-association patterns in large text databases. New Generation Computing. 2000, 28: 49-60.
Wang JL, Chirn GW, Marr T, Shapiro B, Shasha D, Zhang K: Combinatorial pattern discovery for scientific data: some preliminary results. Proceedings of the 1994 ACM SIGMOD International Conference on Management of Data: 24-27 May 1994; Minneapolis, USA. Edited by: Snodgrass, Winslett. 1994, 115-125. full_text. ACM press,
Weiner P: Linear pattern matching algorithms. Proceedings of the 14th IEEE Annual Symposium on Switching and Automata Theory: 15-17 Oct 1973; Iowa, USA. 1973, 1-11. IEEE Computer Society,
McCreight E: A space-economical suffix tree construction algorithm. Journal of the ACM. 1976, 23 (2): 262-272. 10.1145/321941.321946
Ukkonen E: On-line construction of suffix trees. Algorithmica. 1995, 14 (3): 249-269. 10.1007/BF01206331
Apostolico A: The myriad virtues of subword trees. Combinatorial Algorithms on Words, Volume F12 of NATO ASI Series. Edited by: Apostolico, Galil. 1985, 85-96. New York: Springer-Verlag,
Gusfield D: Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology. 1997, Cam-bridge: Cambridge University Press,
Apostolico A, Satta G: Discovering subword associations in strings in time linear in the output size. Journal of Discrete Algorithms. 2009, 7 (2): 227-238. 10.1016/j.jda.2007.02.003
Schieber B, Vishkin U: On finding lowest common ancestors: simplifications and parallelizations. SIAM Journal on Computing. 1988, 17: 1253-1262. 10.1137/0217079
Inenaga S, Bannai H, Hyyrö H, Shinohara A, Takeda M, Nakai K, Miyano S: Finding optimal pairs of cooperative and competing Patterns with bounded distance. Proceedings of the Seventh International Conference on Discovery Science: 2-5 Oct 2004; Padova, Italy. Edited by: Suzuki, Arikawa. 2004, 32-46. Springer, LNAI 3245,
Tompa M, Li N, Bailey T, Church G, De Moor B, Es-kin E, Favorov A, Frith M, Fu Y, Kent W, Makeev V, AA M, Noble W, Pavesi G, Pesole G, Régnier M, Simonis N, Sinha S, Thijs G, van Helden J, Vandenbogaert M, Weng Z, Workman C, Ye C, Zhu Z: Assessing computational tools for the discovery of transcription factor binding sites. Nature Biotechnology. 2005, 23: 137-144. 10.1038/nbt1053
Acknowledgements
Work by Alberto Apostolico was supported in part by the Italian Ministry of University and Research under the Bi-National Project FIRB RBIN04BYZ7, by BSF Grant 2008217, and by the Research Program of Georgia Tech. Work by Cinzia Pizzi was supported in part by Premio di Ricerca "Avere Trent'Anni", Progetto Ateneo of the University of Padova (2008-2010): "Computational Assessment of Protein-Protein Interaction Networks and Validation as a Guide for Modern System Biology", Progetto Cariparo (2008-2011): "Systems Biology Approaches to Infer Gene and Protein Time-series Expression Data", and by Academy of Finland, grant 118653 (ALGODAN). Work by Esko Ukkonen was supported by Academy of Finland, grant 118653 (ALGODAN).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
AA, CP and EU jointly contributed to the conception, design, analysis of the algorithms, and jointly contributed to the writing and editing of the manuscript. Implementation and testing were done by CP. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Apostolico, A., Pizzi, C. & Ukkonen, E. Efficient algorithms for the discovery of gapped factors. Algorithms Mol Biol 6, 5 (2011). https://doi.org/10.1186/1748-7188-6-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1748-7188-6-5








 (see Figure
(see Figure